UNIDAD 3 | artifi-intelk

UNIDAD 3: Representación del conocimiento y razonamiento.

SUBTEMAS

3.1. Sistemas basados en conocimiento.
3.1.1. Concepto de conocimiento.
3.1.2. Lenguajes utilizados en la representación de conocimiento.
3.2. Mapas conceptuales.
3.3. Redes semánticas.
3.4. Lógica de predicados.
3.4.1. Sintaxis.
3.4.2. Semántica.
3.4.3. Validez.
3.4.4. Inferencia.
3.5. Razonamiento con incertidumbre.
3.5.1. Aprendizaje.
3.5.2. Razonamiento probabilístico.

3.5.3. Lógicas multivaluadas.

3.5.4. Lógica difusa.
3.6. Demostración y métodos.

3.1. Sistemas basados en conocimiento.

Los Sistemas Basados en el conocimiento son sistemas avanzados de representación y resolución de problemas complejos. Su arquitectura y sus formalismos de representación son la base de muchos de los sistemas actuales. Su uso se puede encontrar en todas las ramas de aplicaciones especiales de los sistemas informáticos donde se requieran prestaciones especiales, sobre todo en aquellas áreas donde el conocimiento de expertos sea el soporte básico como medicina, industria, gestión, finanzas, organización empresarial y otros.

La naturaleza del conocimiento que contienen es la mayor parte de las veces derivado de la experiencia acumulada en áreas determinadas y la validación de estos sistemas requiere una metodología diferente a la de los sistemas convencionales dada la característica simbólica (y no numérica) del conocimiento que contienen.

3.1.1. Concepto de conocimiento

El conocimiento suele entenderse como:

 Hechos o información adquiridos por un ser vivo a través de la experiencia o la educación, la comprensión teórica o práctica de un asunto de referente a la realidad.
 Lo que se adquiere como información relativa a un campo determinado o a la totalidad del universo.
 Conciencia o familiaridad adquirida por la experiencia de un hecho o situación.
 Incluye el "saber qué", el "saber cómo", el "saber cuándo" y el "saber dónde".

No existe una única definición de "Conocimiento". Sin embargo existen muchas perspectivas desde las que se puede considerar el conocimiento, siendo la consideración de su función y fundamento, un problema histórico de la reflexión filosófica y de la ciencia. La rama de la ciencia que estudia el conocimiento es la epistemología o teoría del conocimiento. La teoría del conocimiento estudia las posibles formas de relación entre el sujeto y el objeto. Se trata por lo tanto del estudio de la función del entendimiento propia de la persona.

El conocimiento es la capacidad que posee el hombre de aprehender información acerca de su entorno y de sí mismo. En el hombre tiene la propiedad de ser sensitivo y suprasensitivo o intelectual, a diferencia del de los animales que sólo abarca el aspecto sensitivo.

El conocimiento humano es sensitivo, ya que son los sentidos los que nos ayudan a obtener experiencias, y suprasensitivo, porque brinda como resultado el razonamiento. Además, posee dos elementos fundamentales: sujeto y objeto; de los cuales el primero es el encargado de captar al segundo y obtener sus propiedades sensibles

3.1.2. Lenguajes utilizados en la representación de conocimiento.

En el caso de los sistemas basados en conocimiento, el lenguaje en el que se expresa la ontología debe reunir características que a veces (dependiendo del dominio) no es fácil compatibilizar:

 Sintaxis formalizada, para poder diseñar sobre bases sólidas un procesador (lo que en sistemas expertos se llama tradicionalmente motor de inferencias.
 Semántica bien definida y que permita la implementación procedimental en el procesador de algoritmos de razonamiento eficientes.
 Desde el punto de vista pragmático, expresividad suficiente para representar de la manera menos forzada posible el conocimiento. Esto significa que, para una determinada conceptuación, el lenguaje con el que se construyen los modelos en el nivel simbólico debe permitir una interpretación declarativa que represente todos los aspectos de esa conceptuación. En la práctica puede ocurrir que no encontremos el lenguaje ideal, y tengamos que forzar la conceptuación para que se ajuste al lenguaje elegido.

Hay lenguajes formales, o teóricos, que satisfacen en mayor o menor grado esas condiciones y lenguajes de implementación, o prácticos, que, siguiendo el modelo de algún lenguaje formal, están adaptados para mecanizar la construcción de ontologías. Nos centraremos en los primeros, que son relativamente estables, y sobre los que se basan los segundos, algunos muy volátiles. Por ejemplo:

 Prolog es un lenguaje de implementación de la lógica de primer orden, que en sus versiones más recientes incluye también construcciones para la programación con restricciones.
 OWL (Web Ontology Language) es un lenguaje de ontolologías para la web basado en una lógica de descripciones (en realidad, son tres sublenguajes). Procede de la fusión de otros dos elaborados independientemente alrededor del año 2000: DAML (DARPA Agent Markup Language, de la Agencia de proyectos del Ministerio de Defensa USA) y OIL (Ontology Inference Layer, de un consorcio formado en el marco de los programas de la U.E.). En 2001 se formó un comité conjunto que hizo una propuesta al Consorcio Web (W3C), y éste publicó el estándar (Proposed Recommendation en la terminología del W3C) en 2003, modificado el 10 de febrero de 2004. Existen numerosas propuestas de mejoras y modificaciones.

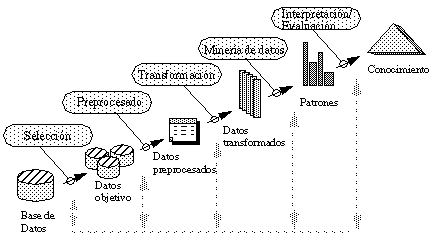
3.2. Mapas conceptuales.

Los mapas conceptuales son herramientas para la organización y representación del conocimiento. Tienen su origen en las teorías sobre la psicología del aprendizaje de David Ausubel enunciadas en los años sesenta.

Este instrumento educativo fue ideado por Joseph Novak en los años 70´s, como una forma de poner en práctica las teorías de David Ausubel sobre aprendizaje signi-ficativo. Los mapas conceptuales son un medio para la representación de proposiciones a través de conceptos formados mediante palabras de enlace que forman relaciones jerárquicas.

También es una técnica, método o recurso esquemático para representar un conjunto de significados conceptuales incluidos en una estructura de proposiciones que tiene por objeto representar las relaciones significativas entre los conceptos y el conocimiento previo del sujeto.

Un mapa conceptual debe contar con los siguientes elementos según Novak:

• Conceptos: Constructos mentales, abstracciones que se pueden emplear para clasificar los distintos objetos del mundo exterior e interior.
• Palabras de enlace: Son los artículos que permiten formar una relación entre los conceptos para formar frases con significados.
• Las proposiciones: Son dos o más términos conceptuales unidos por palabras de enlace que forman unidades semánticas.
• Líneas o líneas de unión: Son aquellas que se utilizan para unir los conceptos y que acompañan a las palabras de enlace.

El mapa conceptual como técnica de aprendizaje tiene importantes repercusiones en el ámbito afectivo-relacional del estudiante, ya que su atención y aceptación favorece el desarrollo de su autoestima. Los mapas conceptuales pueden ser utilizados en diferentes etapas del proceso de enseñanza y aprendizaje (PEA):

• Fomentar el metaconocimiento del estudiante. Son útiles para que el estudiante reaexione en torno a los conocimientos adquiridos así como su punto de partida ante la generación de nuevos conocimientos.

• Extracción de conceptos relevantes. Ayudan al que aprende ya que permite hacer más evidentes los conceptos clave o las proposiciones, así como las conexiones entre estos nuevos conocimientos.

• Fomentan el aprendizaje cooperativo. Permiten el intercambio de ideas y la conformación de significados compartidos, centrando el esfuerzo en construir un nuevo conocimiento. Para aprender el significado de cualquier conocimiento es preciso dialogar, intercambiar, compartir y a veces llegar a un compromiso.

• Instrumento de evaluación. Los mapas conceptuales son herramientas muy útiles a la hora de recopilar información acerca de lo que los estudiantes saben. En general, presentan una radiografía bastante interesante acerca de lo que el estudiante conoce acerca de un concepto determinado.

3.3. Redes semánticas.

Esencialmente es una técnica de conocimiento que permite representar:

 Objetos.
 Eventos.
 Jerarquías.
 Conceptos.
Su descripción simbólica consta de objetos y relaciones, ilustrándose en forma de red.

Descripción

Cada objeto representa a una entidad específica o conjunto de ellas, representándola por medio de una “lista de propiedades” compuestas por listas que contienen parejas “atributo-valor”.

(Mamífero (Nace en Placenta) (Tiene Mamas) (IS-A Animal)...)
(Herbívoro (Come Verdura) (IS-A Mamífero)...)
(Carnívoro (Come Carne) (IS-A Mamífero)...)
(Felino (Facilidad para Trepar) (IS-A Carnívoro)...)
(Gato (Es doméstico) (IS-A Felino)...)

3.4. Lógica de predicados.

La lógica de primer orden, también llamada lógica de predicados o cálculo de predicados, es un sistema formal diseñado para estudiar la inferencia en los lenguajes de primer orden. Los lenguajes de primer orden son, a su vez, lenguajes formales con cuantificadores que alcanzan sólo a variables de individuo, y con predicados y funciones cuyos argumentos son sólo constantes o variables de individuo.

El cálculo de predicados representa una extensión de la lógica proposicional. Sus elementos fundamentales son el objeto y el predicado. Un predicado es simplemente una declaración acerca del objeto, o una relación que el objeto posee. Los predicados pueden combinarse mediante el uso de los operadores lógicos. Algunos ejemplos del uso del cálculo de predicados son:

 Mamífero (perro), que es interpretado como “Un perro es mamífero”.

 Hermana (Ana, Juan), que se interpreta como “Ana es hermana de Juan”.
 Hermana (Ana, Juan) and prima (Ana, Alfredo), se lee como “Ana es hermana de Juan y prima de Alfredo”.

Los elementos del cálculo de predicados

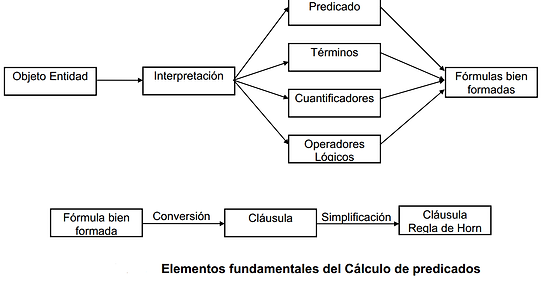
La técnica del cálculo de predicados se caracteriza por:

 -Apoyarse en el formalismo de lógica matemática.
 -Popularidad y explotación.
 -Definición de las expresiones para indicar su veracidad o falsedad.
 -Certeza, dado A → B, A ≦ B no permite el caso de que con premisas válidas se obtengan conclusiones erróneas.

3.4.1. Sintaxis.

El alfabeto del lenguaje formal Q consta de los siguientes símbolos:

a x f P * ' ¬ ∧ ∨ → ↔ ∀ ∃ ( )

A partir de estos símbolos, se definen las siguientes nociones: 

- Un nombre (o constante de individuo) es una a seguida de una o más comillas. Por ejemplo, a', a'' y a'''''' son nombres. Para facilitar la lectura, se suelen omitir las comillas y utilizar distintas letras cerca del comienzo del alfabeto latino, con o sin subíndices, para distinguir nombres distintos: a, b, c, d, e, a1, a3, c9, etc. 

- Una variable (o variable de individuo) es una x seguida de una o más comillas. Por ejemplo, x', x'' y x'''''' son variables. Para facilitar la lectura, se suelen omitir las comillas y utilizar distintas letras cerca del final del alfabeto latino, con o sin subíndices, para distinguir variables distintas: x, y, z, x1, x3, z9, etc. 

- Una función es una f seguida de uno o más asteriscos, y luego de una o más comillas. Por ejemplo, f *', f **'''' y f ****'' son funciones. El número de asteriscos indica la paridad de la función. Para facilitar la lectura, se suelen omitir los asteriscos y las comillas y utilizar distintas letras del alfabeto latino cerca de la f, con o sin subíndices, para distinguir funciones distintas: f, g, h, f1, f3, h9, etc.

 - Un predicado es una P seguida de uno o más asteriscos, y luego de una o más comillas. Por ejemplo, P *', P **'''' y P ****'' son predicados. El número de asteriscos indica la paridad del predicado. Para facilitar la lectura, se suelen omitir los asteriscos y las comillas y utilizar distintas letras en mayúscula a lo largo del alfabeto latino para distinguir predicados distintos: P, A, B, C, S, T, etc.

3.4.2. Semántica.

Una interpretación es un par <D,I>, donde D es un conjunto no vacío llamado el dominio de discurso I es una función llamada la función de interpretación definida como sigue:

1. Si a es un nombre, entonces I le asigna un elemento del dominio.

2. Si f es un función de paridad n, entonces I le asigna una función de n argumentos que toma elementos del dominio y devuelve elementos del dominio.

3. Si P es un predicado de paridad n, entonces I le asigna un conjunto de n-tuplas construidas a partir del dominio.

Luego es posible definir la noción de verdad para una interpretación (para las oraciones de Q):7

1. P(t1,...,tn) es verdadera para la interpretación M si y sólo si la n-tupla formada por las interpretaciones de t1,...,tn es un elemento de la interpretación de P.

2. ¬A es verdadera para la interpretación M si y sólo si A es falsa bajo esa interpretación.

3. (A ∧ B) es verdadera para la interpretación M si y sólo si A es verdadera y B es verdadera bajo esa interpretación.

4. (A ∨ B) es verdadera para la interpretación M si y sólo si A es verdadera o B es verdadera bajo esa interpretación.

5. (A → B) es verdadera para la interpretación M si y sólo si A es falsa o B es verdadera bajo esa interpretación. 6. (A ↔ B) es verdadera para la interpretación M si y sólo si A y B son ambas verdaderas o ambas falsas bajo esa interpretación.

Para dar las definiciones de verdad para fórmulas con la forma ∀x A o ∃x A, primero son necesarias algunas definiciones preliminares: Sea A(x/a) el resultado de reemplazar toda aparición de xen A por un nombre a (que no haya sido utilizado en la fórmula). Además, si M y M' son interpretaciones y a un nombre, entonces M' es una a-variante de M si y sólo si M' es idéntica a M o difiere sólo en el elemento del dominio que le asigna al nombre a.8

3.4.3. Validez.

Las tablas de verdad sirven no solo para definir los conectores, sino también para probar la validez de las oraciones. Si se desea considerar una oración, se construye una tabla de verdad con una hilera por cada una de las posibles combinaciones de valores de verdad correspondientes a los signos propositivos de la oración. Se calcula el valor de verdad de toda la oración, en cada una de las hileras. Si la oración es verdadera en cada una de las hileras, la oración es válida.

EJEMPLO:

3.4.4. Inferencia.

La lógica de primer orden tiene dos reglas de inferencia. La primera es el modus ponens, heredada de la lógica proposicional. La segunda es la regla de Generalización universal, que es característica de la lógica de primer orden. La misma dice:

O en la notación del cálculo de secuentes:

Es decir: a partir de A es posible concluir que ∀x A.

3.5. Razonamiento con incertidumbre.

Ser capaz de razonar sin tener todo el conocimiento relevante en un campo determinado utilizando lo mejor posible el conocimiento que se tiene.

 Es difícil cumplir estos requerimientos utilizando la lógica de primer orden.
 Deben de introducirse modelos para manejar información vaga, incierta, incompleta y contradictoria.
 Crucial para un sistema funcione en el “mundo real”.

3.5.1. Aprendizaje.

El aprendizaje es el proceso a través del cual se adquieren o modifican habilidades, destrezas, conocimientos, conductas o valores como resultado del estudio, la experiencia, la instrucción, el razonamiento y la observación. Este proceso puede ser analizado desde distintas perspectivas, por lo que existen distintas teorías del aprendizaje. El aprendizaje es una de las funciones mentales más importantes en humanos, animales y sistemas artificiales.

Tipos de Aprendizaje

• Habituación. Una Respuesta que decae ante un Conjunto de Estímulos Repetidos (o Continuos) No Asociados a Ningún Tipo de Recompensa o Refuerzo. Implica Tendencia a Borrar todo Tipo de Respuesta ante un Estímulo que No tiene Importancia para la Supervivencia. Sirve como Filtro a un Conjunto de Estímulos No Relevantes.

• Asociativo. Un Evento permite Predecir, con cierta confianza, la Ocurrencia (o no) de otro. Un Animal que Conoce estas Relaciones pueden sacar provecho Anticipándose a esos Eventos y Comportarse apropiadamente.

• Condicionamiento. Un Animal adquiere la Capacidad de Responder a un Estímulo Determinado con la misma Acción Refleja con que Respondería a otro Estímulo Condicionante (Refuerzo o Recompensa) cuando ambos Estímulos se presentan Concurrentemente (o sobre puestos en una Secuencia) un cierto número de veces.

• Prueba y Error. Los Animales permanecen siempre Activos y su Atención se fija Primero aquí y luego allá probando todas las Posibilidades inimaginables hasta que de manera más o menos Accidental resuelve con Éxito la Tarea y Obtiene Recompensa. Requiere la Existencia del Refuerzo (o Recompensa) para animar la Selección de la Respuesta Deseada.

• Latente. Tiene lugar en Ausencia de Recompensa. Se aprende algo que permanece Latente hasta que es Necesario.

•Imitación. Implica Copiar una Conducta, Acción o Expresión Nueva o que resulta Imprescindible de Aprender si no es Copiada de otro Individuo.

• Impronta. La Manera en que un Rango Específico de Estímulos es Capaz de Elicitar una Respuesta pudiendo ser Limitado y Refinado mediante la Experiencia. Su Duración se Restringe a Periodos Sensitivos.

3.5.2. Razonamiento probabilístico.

La ventaja del razonamiento probabilístico en comparación con el razonamiento lógico reside en que el agente lógico puede tomar decisiones racionales aún sin disponer de suficiente información para probar que una acción dada funcionará.

Para representar la dependencia que existe entre determinadas variables se usa una estructura de datos conocida como RED DE CREENCIAS y también para especificar de forma concisa la distribución de probabilidad conjunta. Esta red es una gráfica que consta de:

 Los nodos están formados por un conjunto de variables aleatorias
 La conexión de cada nodo significa que el nodo X ejerce una influencia directa sobre Y
 Por cada nodo hay una tabla de probabilidad condicional que sirve para cuantificar los efectos de los padres sobre el nodo.
 La gráfica es acíclica, es decir, no tiene grafos dirigidos.

3.5.3. Lógicas multivaluadas.

Un argumento es lógicamente válido si es lógicamente imposible que sus premisas sean todas verdaderas y la conclusión falsa, es decir, si es lógicamente necesario que si las premisas son todas verdaderas, la conclusión también lo sea. En estos casos, también se dice que la verdad se transmite de las premisas a la conclusión. La verdad de la conclusión se sigue de la verdad de las premisas.

Definiciones

Valores semánticos, valores destacados.
 Interpretación: Una función que asocia un significado (valor semántico) a cada fbf.
 Modelo para A: Una interpretación que asigna a A un valor destacado.
 Formula valida: aquella para la que toda interpretación es un modelo.
 Inferencia: De un conjunto S se infiere A si todo modelo de S también lo es de A.

La lógica multivariada se ha usado en matemáticas como procedimiento para buscar modelos no estándar; esto es esencialmente lo que se hace para conseguir los modelos generales de Henkin para la lógica superior, responsables de su teorema de completud. Puede resultar también útil para entender la lógica dinámica de dos formas distintas:

1. la lógica dinámica proposicional se traduce a la lógica multivariada por un procedimiento claramente deudor al de Henkin y esta también
2. la lógica dinámica no-estándar, heredera igualmente de los modelos generales de Henkin.

3.5.4. Lógica difusa.

La lógica difusa (tambien llamada lógica borrosa o lógica heurística) se basa en lo relativo de lo observado como posición diferencial. Este tipo de lógica toma dos valores aleatorios, pero contextualizados y referidos entre sí. Así, por ejemplo, una persona que mida 2 metros es claramente una persona alta, si previamente se ha tomado el valor de persona baja y se ha establecido en 1 metro. Ambos valores están contextualizados a personas y referidos a una medida métrica lineal.

A lógica difusa ("fuzzy logic" en inglés) se adapta mejor al mundo real en el que vivimos, e incluso puede comprender y funcionar con nuestras expresiones, del tipo "hace mucho calor", "no es muy alto", "el ritmo del corazón está un poco acelerado", etc.

La clave de esta adaptación al lenguaje, se basa en comprender los cuantificadores de nuestro lenguaje (en los ejemplos de arriba "mucho", "muy" y "un poco"). En la teoría de conjuntos difusos se definen también las operaciones de unión, intersección, diferencia, negación o complemento, y otras operaciones sobre conjuntos (ver también subconjunto difuso), en los que se basa esta lógica.

Un esquema de funcionamiento típico para un sistema difuso podría ser de la siguiente manera: