UNIDAD 2 | artifi-intelk

UNIDAD 2: Técnicas de Búsqueda.

SUBTEMAS

2.1. Solución de problemas con búsqueda.
2.2. Espacios de estados.
2.2.1. Determinísticos.
2.2.2. No determinísticos.
2.3. Métodos de búsqueda.
2.3.1. Primero en anchura (breadthfirst).
2.3.2. Primero en profundidad (depthfirst).
2.3.3. Grafos O.
2.3.4. Grafos A.
2.4. Satisfacción de restricciones.
2.5. Teoría de juegos.

2.1. Solución de problemas con búsqueda.

Definición formal del problema:

El primer paso para diseñar un programa que resuelva un problema es crear una descripción formal y manejable del propio problema. Sería adecuado contar con programas que produzcan descripciones formales a partir de descripciones informales, proceso denominado operacionalización. Dado que por ahora no se conoce la forma de construir estos programas este proceso debe hacerse manualmente.

Hay problemas que por ser artiﬁciales y estructurados son fáciles de especiﬁcar (por ejemplo el ajedrez, el problema de las jarras de agua, etc.). Otros problemas naturales, como por ejemplo la comprensión del lenguaje, no son tan sencillos de especiﬁcar.

Para producir una especiﬁcación formal de un problema se deben deﬁnir:

-Espacio de estados válidos.

-Estado inicial del problema.

-Estado objetivo o ﬁnal.

Reglas que se pueden aplicar para pasar de un estado a otro.

-La representación como espacio de estados forma parte de la mayoría de los métodos de Inteligencia Artiﬁcial(IA). Su estructura se corresponde con la resolución de problemas porque:

-Permite deﬁnir formalmente el problema, mediante la necesidad de convertir una situación dada en una situación deseada mediante un conjunto de operaciones permitidas;

-Permite deﬁnir el proceso de resolución de un problema como una combinación de técnicas conocidas y búsqueda (la técnica general de exploración del espacio intenta encontrar alguna ruta desde el estado actual hasta un estado objetivo).

Análisis del problema

Luego de deﬁnir el problema formalmente, el segundo paso en la resolución del problema es el análisis del mismo. A ﬁn de poder elegir el método más apropiado para resolver un problema particular, es necesario analizar distintas cuestiones que afectan a la deﬁnición del mismo y a las caracterśticas de la solución deseada. Existen varias preguntas a responder acerca del problema:

-¿Puede descomponerse el problema en subproblemas más pequeños?
-¿Pueden deshacerse pasos inadecuados hacia la solución?
-¿Es predecible el universo del problema?
-¿Una solución es buena de manera absoluta o relativa?
-¿La solución deseada es un estado o la ruta hacia un estado?
-¿El conocimiento se necesita para resolver el problema o para restringir la búsqueda de la solución?

El programa que soluciona el problema ¿busca la solución solo o necesita interactuar con una persona?

-¿Puede descomponerse el problema en subproblemas más pequeños?

Algunos problemas pueden descomponerse en subproblemas independientes, de manera que encontrar una solución global es la composición de soluciones particulares. Por ej. en la resolución de integrales, una integral puede descomponerse por partes, y resolver las partes simples directamente o descomponerlas recursivamente.

Por otra parte, existen otros problemas que no pueden descomponerse y componer la solución a partir de las soluciones parciales de sus partes p. ej. problemas de planiﬁcación de rutas con restricciones o el mundo de los bloques. Por el contrario, una solución necesita considerar globalmente el problema.

¿Pueden deshacerse pasos inadecuados hacia la solución?

Algunos problemas permiten deshacer uno o varios pasos hacia una solución una vez realizados. En este aspecto, existen tres categorías en las que puede dividirse un problema:

Recuperables: en un punto dado es posible deshacer todos los pasos inadecuados hacia la solución.Por ejemplo en el juego 8-puzzle. La estructura de control se implementa con una pila en la que se almacenan las decisiones para poder volver atrás.

No recuperables: en un punto dado no es posible deshacer ningún paso realizado. Por ejemplo en una partida de ajedrez no se puede volver atrás una vez movidas las piezas. En estos problemas el sistema debe esforzarse en la toma de decisiones pues éstas son irrevocables. Algunos usan una planiﬁcación en la que se analiza por adelantado una secuencia de pasos antes de realizar el primer paso para descubrir a donde conduce.

Ignorables: en un punto dado es posible ignorar los pasos realizados hasta el momento y comenzar de nuevo con una nueva solución. Por ej. un demostrador de teoremas puede abandonar una demostración basada en un lema dado y comenzar nuevamente. Estos problemas se resuelven con estrategias de control sencillas que nunca vuelven hacia atrás.

-¿Es predecible el universo del problema?

Los problemas pueden ser de:

Consecuencia cierta: es posible planiﬁcar una secuencia de movimientos estando seguros del resultado a obtener. Se puede realizar una planiﬁcación para generar operadores que garanticen llegar a la solución.

Consecuencia incierta: no es posible planiﬁcar con certeza pues no se sabe que ocurrirá luego del siguiente movimiento. Sin embargo, se puede realizar una planiﬁcación para generar operadores que tengan una buena probabilidad de llegar a la solución.

Los problemas más difíciles de resolver son los no recuperables de consecuencia incierta. Por ejemplo el control del brazo de un robot: es de consecuencia incierta pues alguien puede interponer un objeto en la ruta del brazo, se puede atascar, etc.

-¿Una solución es buena de manera absoluta o relativa? La solución de un problema puede consistir en encontrar:

Algún camino: sólo importa encontrar una solución sin importar si existen otros caminos que conducen a la solución. Generalmente se resuelven con heurísticas. Por ejemplo programa de respuestas a preguntas.

El mejor camino: importa encontrar la ruta más corta hacia la solución. Son problemas más complicados de computar. Algunos requieren una búsqueda más exhaustiva que usando heurísticas. Por ejemplo en el problema del viajero importa encontrar la ruta más corta entre las ciudades a visitar.

-¿La solución deseada es un estado o la ruta hacia un estado? La solución de un problema puede consistir en encontrar:

Un estado ﬁnal: no es necesario el registro del proceso seguido, sólo importa arribar a la solución ﬁnal. Por ejemplo interpretar texto.

Una ruta hacia un estado ﬁnal: se necesita dar el camino seguido desde el estado inicial al estado ﬁnal. Por ejemplo problema de las jarras de agua.

-¿El conocimiento se necesita para resolver el problema o para restringir la búsqueda de la solución?

El conocimiento puede emplearse para:

Reconocer la solución: se necesita gran cantidad de conocimiento acerca del problema para poder encontrar una solución. Por ejemplo comprensión de texto.

Acotar la búsqueda: la solución básica puede encontrarse con poco conocimiento, pero para restringir el árbol de búsqueda y encontrar la solución de manera más eﬁciente es necesario contar más conocimiento. Por ejemplo en el ajedrez se necesita básicamente poco conocimiento para conocer los movimientos legales y un mecanismo sencillo de búsqueda. Pero dado que para aumentar la eﬁciencia de la búsqueda ésta debe restringirse, se necesita conocimiento de heurísticas de buenas estrategias y tácticas para jugar.

El programa que soluciona el problema ¿busca la solución solo o necesita interactuar con una persona?

Con respecto a la relación programa-usuario, existen dos tipos de programas que solucionan el problema:

Solitarios: reciben como entrada el problema y dan como salida la solución. No importa el razonamiento que haya seguido la máquina para encontrar la solución. Por ejemplo problema de las jarras de agua.

Conversacionales: existe una comunicación hombre-máquina de manera que el usuario puede ayudar a la máquina o la máquina puede informar al usuario durante la búsqueda de la solución. Para que esta comunicación sea posible debe existir una correspondencia entre el razonamiento seguido por la máquina y la forma de razonamiento humano. Por ej. en un sistema experto de diagnóstico médico, el usuario no aceptaría el veredicto de una máquina si no puede comprender el razonamiento que la llevó a él, o un simple juego como buscaminas.

2.2 Espacios de estado.

El espacio de estados es la representación de un problema que abarca todas las posibles situaciones que se pueden presentar en la solución del problema.

Los espacios de estados implícitos normalmente utilizan un sistema de producción para generar sobre la marcha los posibles estados siguientes de un estado dado. Los juegos suelen crear un espacio de estados implícito ya que un juego puede variar dependiendo de las reglas que lo describen.

Los espacios de estados explícitos son aquellos en los se define, previo al inicio de la búsqueda, todos los estados posibles y las conexiones entre ellos.

La representación de los espacios de estados explícitos se puede dar o no determinísticamente.

2.2.1. Determinísticos.

La representación de los espacios de estados explícitos se puede dar o no determinísticamente, esto es, que el espacio de estados determinísticos contienen un único estado inicial y seguir la secuencia de estados para la solución

Los espacios de estados determinísticos son usados por los sistemas expertos.

2.2.2 No determinísticos.

El no determinístico contiene un amplio número de estados iniciales y sigue la secuencia de estados perteneciente al estado inicial del espacio.

Los no determinísticos son usados por sistemas de lógica difusa.

2.3.- Métodos de búsqueda

Los métodos de búsqueda son una serie de esquemas de representación del conocimiento, que mediante diversos algoritmos nos permite resolver ciertos problemas desde el punto de vista de la I.A.

Los elementos que integran los métodos de búsqueda son:

 Conjunto de estados: todas las configuraciones posibles en el dominio.
 Estados iniciales: estados desde los que partimos.
 Estados finales: las soluciones del problema.
 Operadores: se aplican para pasar de un estado a otro.
 Solucionador: mecanismo que nos permite evolucionar de un estado a otro mediante un algoritmo aplicando los siguientes pasos:

1. Elegir el estado a explorar.

2. Establecer un operador que trabaje sobre el estado elegido en el paso 1.
3. Comprobar si el resultado obtenido es un estado final (es una solución del problema). Sino ir al paso 1.

Ejemplo con 8-puzzle: este juego consiste en, dada una matriz de 3x3 elementos, tenemos 8 números que deben de ser ordenados dejando la casilla central vacía.

Para resolverlo usaremos técnicas de búsqueda:

-El conjunto de estados son todas las combinaciones posibles de ordenación de las 9 piezas.

-El estado inicial es el estado en el que nos dan el puzzle, en desorden.
-El estado final es el puzzle ordenado.
-Los operadores son mover una ficha en cualquier dirección: arriba, abajo, izquierda o derecha.

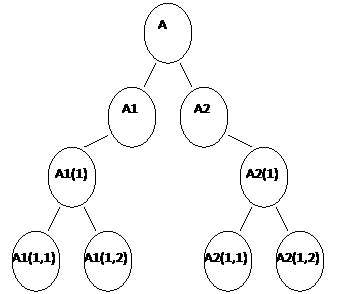
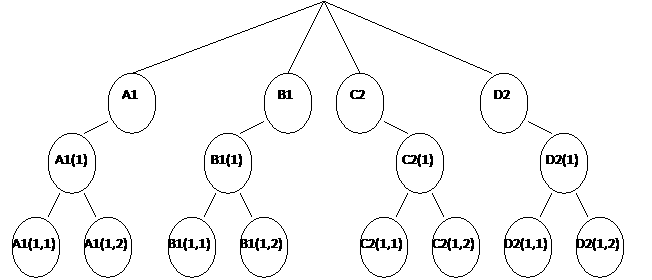
2.3.1- Primero en anchura (breadth-first)

Búsqueda en anchura:

 -Procedimientos de búsqueda nivel a nivel.
 -Para cada uno de los nodos de un nivel se aplican todos los posibles operadores.
 -No se expande ningún nodo de un nivel antes de haber expandido todos los del nivel anterior.
 -Se implementa con una estructura FIFO.

Ejemplo de movimiento de caballo dirigido con búsqueda en anchura.

Ventajas:

 Si existe la solución, la encuentra en la menor profundidad posible.
Desventajas:
 Explosión combinatoria aparece frecuentemente debido a la alta complejidad espacial y temporal de esta técnica.

2.3.2- Primero en profundidad (depth-first)

Búsqueda en profundidad:
 -La búsqueda se realiza por una sola rama del árbol hasta encontrar una solución o hasta que se tome la decisión de terminar la búsqueda por esa dirección.
-Terminar la búsqueda por una dirección se debe a no haber posibles operadores que aplicar sobre el nodo hoja o por haber alcanzado un nivel de profundidad muy grande.
-Si esto ocurre se produce una vuelta atrás (backtracking) y se sigue por otra rama hasta visitar todas las ramas del árbol si es necesario.

Ventajas:
 Tiene menor complejidad espacial que búsqueda en amplitud.

Desventajas:
 Se pueden encontrar soluciones que están más alejadas de la raíz que otras.
 Existe el riesgo de presencia de bucles infinitos.

Búsqueda en profundidad progresiva:

 Se define una profundidad predefinida.
 Se desarrolla el árbol realizando una búsqueda en profundidad hasta el límite definido en el punto anterior.
 Si se encuentra la solución - FIN
 En caso contrario, se establece un nuevo límite y volvemos al segundo paso.

2.3.3- Grafos O

Este algoritmo, combina las ventajas de los algoritmos primero en profundidad y primero en amplitud. Sigue un sendero a la vez, pero puede cambiarse a otro sendero que parece más prometedor que el que está siguiendo.

En este sentido, puede considerarse que es un algoritmo que realiza su proceso de búsqueda en un grafo de tipo O, ya que todos sus ramales representan una alternativa de solución. Para su operación, el algoritmo necesita dos listas de nodos y una función heurística que estime los méritos de cada nodo que se genere:

1. ABIERTOS - Es una variable que contiene los nodos que han sido generados. La función heurística ha sido aplicada a ellos, pero todavía no han sido examinados, es decir no se han generado sus sucesores. ABIERTOS puede considerarse como una COLA DE PRIORIDADES en la que los elementos con mayor prioridad son los que tienen los valores más prometedores, dados por la función heurística.

2. CERRADOS - Es una variable que contiene los nodos que han sido examinados. Es necesario tener esta información, para que la búsqueda sea en un grafo y no en un árbol.

3. FUNCIÓN HEURÍSTICA - Permite que el algoritmo busque primero por senderos que son o parecen más prometedores.

Para muchas aplicaciones, es conveniente definir esta función f', como la suma de dos, que se las llamará g y h'. La función g es una medida del costo de llegar desde el nodo inicial al nodo actual. La función h' es una estimación del costo adicional para llegar desde el nodo actual al estado objetivo. Aquí es donde se explota el conocimiento que se dispone sobre el dominio del problema.

Es decir, la función combinada f' representa una estimación del costo de llegar desde el estado inicial hasta el estado objetivo, siguiendo el sendero que ha generado el nodo actual. Si el nodo actual ha generado más de un sendero, el algoritmo deberá dejar registrado sólo el mejor.

El algoritmo, en la forma que fue formulado, se aplica a grafos. Puede ser simplificado para aplicarse a árboles, si no se preocupa de comprobar si un nuevo nodo está en ABIERTOS o en CERRADOS. Esto aceleraría la generación de nodos y la búsqueda, para casos en que es poco probable que se repitan nodos.

Usualmente, el costo de ir de un nodo a su sucesor, g, se fija en una constante igual 1, cuando se desea encontrar un sendero a la solución, que involucre el menor número de pasos. Si por el contrario nos interesa encontrar el camino menos costoso y algunos operadores cuestan más que otros, se asume un valor de g, que refleje esos costos. Un valor de g igual a cero significaría que simplemente nos interesa llegar a alguna solución, de cualquier manera.

Si h' es un estimador perfecto de h, hará que A* converja inmediatamente al objetivo, sin búsqueda. Mientras mejor sea h', más cerca se estará de alcanzar esta aproximación directa. Si h' vale cero, la búsqueda será controlada por g. Si el valor de g es también cero, hará que la búsqueda sea aleatoria. Si el valor de g es siempre 1, hará que la búsqueda sea primero en anchura. Para los casos en que h' no sea perfecto ni cero, y nunca llega a sobrestimar el valor de h, el algoritmo A* está garantizado que encontrará un sendero óptimo a un objetivo, en caso de que exista solución. Cuando un algoritmo garantiza el encontrar una solución óptima, si esta existe, se dice que es admisible.

2.3.4- Grafos A

 Metodología: Ponderar a la vez lo cerca que estamos del nodo meta y lo lejos que estamos del nodo inicial.
 Tipo: tentativo.
 Ventajas: soluciones más cercanas a la raíz.
 Inconvenientes: la función de evaluación se complica.

2.4.- Satisfacción de restricciones

Entre las muchas extensiones que se han propuesto para Prolog la que más impacto ha tenido (hasta el punto de que prácticamente todas las implementaciones que se vienen haciendo en los últimos años la incluyen) es la de introducir mecanismos para resolución de problemas de satisfacción de restricciones. A esta ampliación se le llama programación lógica con restricciones, o, abreviadamente, CLP (Constraint Logic Programming).

En primer lugar es interesante observar que la búsqueda de soluciones en Prolog es en sí misma un problema de satisfacción de restricciones: se trata de buscar valores para las variables que sean compatibles con las restricciones impuestas por las cláusulas.

Algunos problemas sencillos pueden expresarse en Prolog puro, haciendo uso de los predicados incorporados «=» , «>» , etc. Por ejemplo, para el coloreado del mapa de la Figura con tres colores podemos escribir:}

color(rojo).

color(verde).
color(azul).
coloreado(A,B,C,D) :-
        satisface_restr(A,B,C,D),
        color(A), color(B), color(C), color(D).
satisface_restr(A,B,C,D) :-
        noig(A,B), noig(A,C), noig(A,D),
        noig(B,C), noig(B,D), noig(C,D).
noig(X,Y) :- X\=Y.

En CLP se consideran variables con dominios finitos, y se utiliza otro operador para la restricción de desigualdad entre dos variables que : X##Y. El procesador sólo evalúa esta condición cuando una de las dos variables tiene asignado un valor, y entonces elimina ese valor del dominio de la otra. Naturalmente, es necesaria otra construcción sintáctica para declarar los dominios de las variables.

Los componentes del estado, son equivalentes a un grafo de restricciones, los cuales están compuestos de:

Variables. Dominios (valores posibles para las variables).
Restricciones (binarias) entre las variables.

Objetivo: encontrar un estado (una asignación completa de valores a las variables) Que satisface las restricciones.

Ejemplos:

 Crucigramas.
 Colorear mapas.

2.5.- Teoría de juegos:

La Teoría de Juegos es un tipo de análisis matemático orientado a predecir cuál será el resultado cierto o más probable de una disputa entre dos o más individuos o empresas o países, etc. En el mundo real son muy frecuentes las situaciones en las que, al igual que en los juegos, su resultado depende de la conjunción de decisiones de los diferentes agentes o jugadores. En la teoría de juegos no tenemos que preguntarnos qué vamos a hacer, tenemos que preguntarnos qué vamos a hacer teniendo en cuenta lo que pensamos que harán los demás y ellos actuarán pensando según crean que van a ser nuestras actuaciones... tales situaciones reciben el nombre de "juegos".

En su fase inicial la teoría de juegos fue utilizada para explicar algunos comportamientos de la economía, pero actualmente es utilizada en otras áreas como el derecho, la biología, la filosofía, la ética, la ciencia política, la informática, la inteligencia artificial o la cibernética. El valor principal de la Teoría de Juegos es que analiza y cuantifica conceptos como la cooperación, la competición y los conflictos interpersonales.

Algunas aplicaciones de la Teoría de Juegos a la vida real son las siguientes: Contratos, Guerras militares o comerciales, Marketing para la competencia en los mercados, Negociaciones domésticas, comerciales o colectivas y Alianzas.

Esta teoría fue diseñada y elaborada a partir de la Segunda Guerra Mundial por John Von Neumann (matemático) y Oscar Morgenstern (economista) en 1944. Durante las dos décadas que siguieron a la guerra uno de los progresos más importantes de la teoría económica fue la Teoría de Juegos y el comportamiento económico.

A principios de los años 50, con una serie de artículos, el matemático John F. Nash, cuya biografía es conocida mediante la película “Una Mente Maravillosa”. Nash logra darle forma matemática al concepto de equilibrio que los economistas usaban durante esa época y demostró la existencia para una gran clase de juegos, con lo que se llamó “Equilibrio de Nash”.

En síntesis, en la Teoría de Juegos nada es fijo. La economía es dinámica y evoluciona. Los jugadores crean nuevos mercados y asumen múltiples papeles. Son innovadores. Nadie adopta los precios y los productos porque sí. Si esto le suena como a libre mercado o a un escenario de mercado rápidamente cambiante, ésta es la razón por la cual la Teoría de Juegos es tan atrayente en la nueva economía.

Una aplicación actual de la Teoría de Juegos está dada en el análisis del poder de decisión de los países de la Unión Europea respecto a la regla de votación incluida en el Tratado de la Constitución Europea, celebrado en Bruselas el 18 de Junio de 2004. Investigadores en Teoría de Juegos, de la Universidad de Sevilla, han presentado una carta a los gobiernos de los Estados miembros de la Unión Europea, puesto que resultados de su investigación han arrojado como conclusión que con dicha regla de votación no se respeta el principio básico de cualquier ciudadano de la Unión Europea que es que tenga el mismo poder de decisión; por ello han propuesto un nuevo sistema de votación.